Roll length calculator

Introduction

Knowing the length of a roll just by measuring its diameter can be useful in many situations, since many everyday objects are in rolled form, like tapes, paper, plastic films, and so on.

There are two ways of calculating the length of roll (mathematically speaking a "spiral"), an exact and complex formula derived from integral calculation and an approximate and simpler formula derived from the sum of circumferences of concentric circles. The approximate formula is enough in many situations as long as the thickness of the tape is small compared to the diameter of the roll.

The calculator

The following calculator will simplify the math and will do the calculations for you (with the exact or the simplified formula):

Mobile version available here.

Derivation of the approximate formula

Now let's have a look on how these formulas are deduced. To keep things simple, let's consider the spiral as a series of concentric circles (one per turn) where the radius increases by the thickness of the tape every turn. The error will be small if the thickness is small compared to the minor diameter of the roll.

Let D₀ be the inner diameter of the roll (the diameter of the core), D₁ the outer diameter of the roll, h the thickness of the tape and N the number of turns. We look for the length of the tape L.

First, the number of turns is easy to compute, since it's just the difference of the two radii divided by the thickness of the tape or, in terms of diameter:

The circumference of the first turn is πD₀, the one of the second turn π(D₀+2h), the one of the third one π(D₀+4h), and so on until the N^th turn, which has a circumference of π(D₀+2(N–1)h). The total length of the tape is therefore:

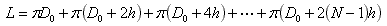
By rearranging the terms we get:

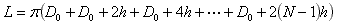
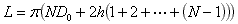
Now, the sum of the integers from 1 to N-1 can be expressed in the form N(N–1)/2 (Gauss's formula). The length L can therefore be expressed as:

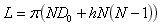
Or, in a simpler form:

Inverting the approximate formula

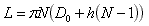
Now, if we want to do the reverse operation, meaning to calculate D₁ as a function of L, we just need to invert this equation (2^nd degree in N) and we get:

Second degree equations usually have two solution, expressed with a "±" sign; but in this case we just want the solution with "+", as the solution with "–" corresponds to the same spiral, but coiled in the other direction.

Than we calculate D₁ with:

Derivation of the exact formula

To calculate the exact length of the spiral, we write the equation of the curve in polar coordinates:

Here ρ is the distance between the axis as a function of the angle φ. φ is expressed in radians and is 0 at the beginning and increases by 2π every turn. So, every turn the radius ρ increases by h.

To calculate φ we proceed as we did before to calculate N, but now we have a factor 2π because of the angle in radians:

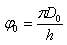and

The length of a curve in polar coordinates is calculated with the following formula:

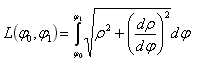
Here, the derivative is easy to calculate and we get:

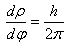
So, to find the exact length, one just has to calculate:

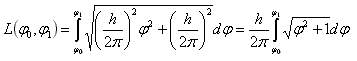
Now, the things are more complicated. Even if a good integral solving list should include the solution of such integral, if we want to calculate it by hand, we'll have first to change the variable using the hyperbolic identity ch²x – sh²x = 1 and than transform the result with another hyperbolic identity: ch(2x) = ch²x + sh²x. After a full page of algebra we get the exact length:

Inverting the exact formula

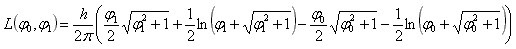
Inverting this function is not easy, and in this application a numerical approximation (the Newton's method) is used. This method start with an approximation or a guess of the solution (zero of a function) and iteratively refines it by finding the intercept point on the abscise axis of its tangent line. Since this point is a better approximation, so the process can be repeated until the desired precision is achieved.

Here we have L(φ₀,φ₁)=L₀ and we want to find φ₁ knowing L₀ which is the given length of the spiral; φ₀ is constant. We can rewrite this equation in the form L(φ₀,φ₁) – L₀ = 0 and we call it f(φ₀,φ₁) as follows:

The Newton's method tells us that a better approximation of φ₁ is φ'₁ which is:

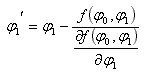
And we can iterate the above equation until the desired precision is achieved. The calculator in this page tries to reach as much precision as it can be stored in a regular JavaScript floating point variable, so that no error can be remarked. Usually a few iterations are enough. To start this algorithm, we can use the approximate formula to find an initial φ₁.

In order to implement this method, we need to compute by hand the derivative ∂f(φ₀,φ₁)/∂φ₁, which is just ∂L(φ₀,φ₁)/∂φ₁ since L₀ is constant. We find:

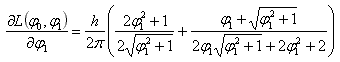
With this the inversion algorithm can be easily implemented in the calculator.

Evaluation of the error of the approximate formula

To have an idea of the error introduced by the approximate formula, let's take an example: suppose we have a roll of paper with an inner diameter D₀ = 100 mm, an outer diameter D₁ = 200 mm and a thickness h = 100 μm. With the approximate formula we get N = 500 and L_approx = 235.4623694 m. With the exact formula we get φ₀ = 1000π, φ₁ = 2000π and L_exact = 235.6194545 m. The difference is only 157 mm over 235 m, an error of 0.067 %. If we consider that when we measure the diameter the precision is probably about 1 mm over 1 m (0.1 %) the error of the approximate formula is small.

The advantage of the approximate formula is that it uses only basic operations and can be easily computed even by hand on a simple pocket calculator. The exact formula uses a lot more math, needs at least a good scientific calculator, is long to do by hand and has little gain on precision. On the other hand, on a computer or a smart-phone, there is enough CPU power for this JavaScript calculator to consider the exact formula as a better option.