
Horizontally (left image) and vertically (right image) polarized waves (click to enlarge).
Polarization of light is an important effect in photography. Our eye is (almost) insensitive to polarization, and the majority of the light we observe every day is not polarized. But in some cases, with the help of a polarizer, we can emphasize some specific light and attenuate some other to obtain better (or different) images. A polarizer is an optical filter that transmits only one polarization. This page explains the basic principles of polarization and how to apply it to photography.
Polarization is a property of transversal waves like electromagnetic waves (and light) that can oscillate in a defined orientation. For electromagnetic waves, polarization is always expressed in terms of electric field. This orientation can have any angle, but if it's horizontal or vertical we talk about horizontal or vertical polarization respectively, as illustrated in the two pictures below. This kind of polarization is said to be linear.


Horizontally (left image) and vertically (right image) polarized waves
(click to enlarge).
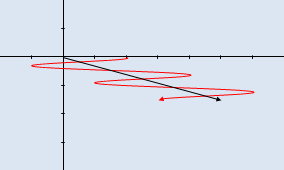
Light can also be circularly polarized, as a result of the superposition of two linear polarization 90° out of phase and oriented at 90° between them (dashed lines). The result is a sort of helix shaped wave, as illustrated in the two pictures below. Circular polarization is rare in nature and, for photography, linear polarization is enough (even if photographer use circular polarizer, as explained below).
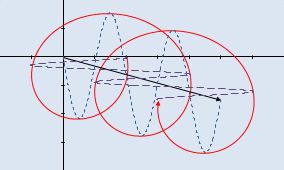
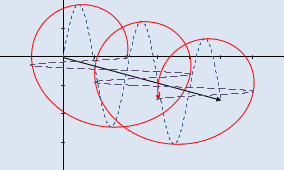
Left-hand and right-hand circular polarized waves, left and right
images respectively (click to enlarge).
When light is said to be non-polarized, it means it's a superposition of many many different waves, each with a different (random) polarization. When this light goes through a polarizer, only one polarization sate (orientation) can go through and theoretically, half of the light is blocked by the polarizer.
There is controversy about the definition of left and right hand circular polarization, since two opposing definitions exist. For regular photography, it's not important to know which exact hand is the circular polarization, and it's usually not specified on common polarizers. If you find that your favorite textbook has a different definition of left and right polarizations, don't worry, you can still shoot good pictures.
A linear polarizer can be imagined like a cooking grid with plenty of parallel thin slots. Waves can only go through the slots if correctly aligned with them. If the polarization of the incident wave is at 90° it will be completely blocked. If both are perfectly aligned all the light will go through. If the angle is in-between, only part of the light will go through. The light emerging from a polarizer is always polarized parallel to the orientation of the polarizer itself. Linear polarizer are reversible: they work the same in either directions (circular polarizers are not). The following images summarize how a linear polarizer works. Non-polarized light is represented by equal arrows in all directions and polarized light by two arrows in the direction of polarization. Round arrows represent the direction of propagation of the light.
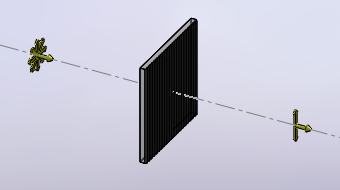
Non-polarized light impinging on a vertical polarizer, vertical
polarization is obtained (click to enlarge).
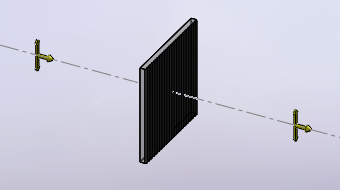
Vertically polarized light impinging on a vertical polarizer, the
light can go through undisturbed (click to enlarge).

Horizontally polarized light impinging on a vertical polarizer, no
light can go through (click to enlarge).
When light scatters on a particle, some light is re-emitted in all directions, but light re-emitted in the plane perpendicular to the incident ray is polarized parallel to this plane, as shown in the below picture, where the gray sphere in the middle represents a particle.
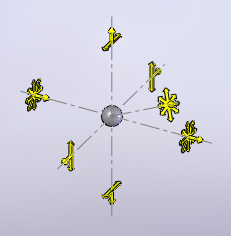
Light scattered by a particle.
Light is coming from the left and scattered in all directions, only a few are
shown.
Light scattered perpendicularly to the incoming ray is linearly polarized
(click to enlarge).
Scattering is complex process depending on wavelength and particle size. It turns out that the sky is composed by particles that scatter more short wavelengths (blue) than long wavelengths (red) and for this reason the sky appears blue. If no scattering existed or the atmosphere wasn't there the sky would be black.
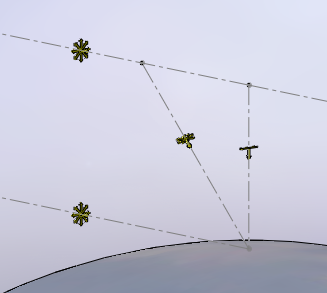
Light scattered by the sky.
Here only two particles are represented showing the light perceived by an
observer on earth.
Light is coming from the sun located very far on the left.
Rays coming from the sun are considered parallel, the ray on the bottom is a
direct ray (click to enlarge).
In the above picture, the earth surface is represented on the bottom and the point on it is an observer. The light is coming from the sun located very far outside the picture on the left. Rays coming from the sun are assumed to be parallel. If an observer looks at the sky while having the sun 90° on his left (or 90° on his right) the light he sees is vertically polarized. Light coming directly from the sun is not polarized because it wasn't scattered perpendicularly to its path, as represented by the bottom ray.
The following picture shows a landscape with blue sky. The left third of the image was taken through a horizontal polarizer, the middle third through a vertical polarizer and the right part without any polarizer. The sun was about 90° on the right of the camera.

A landscape with a blue sky.
Left: horizontal polarizer; middle: vertical polarizer; right: no
polarizer.
35 mm, f/5.6, 1/200 s 1/400 s 1/1000 s (respectively),
ISO-400.
Exposure was adjusted to take into account polarizer losses
(click to enlarge).
As one can see, when the polarizer is horizontal, it blocks part of the vertically polarized blue light of the sky making it appear darker. Water droplets in the white cloud are too big to have a noticeable effect for light wavelengths and stay white, increasing the contrast between the cloud and the sky. If the polarizer is vertical, blue light gets through and the result is quite similar as if no polarizer was used.
The angle between the water surface and the camera is too small to appreciate the effect of polarization due to reflection (see below).
When non-polarized light goes through an ideal perfect linear polarizer, only 50% of the emerges on the other side. Real polarizers have even higher losses and transmission factors around 25% are quite common. In photography terms, this means losing about two stops. The fact that polarizers have a dark gray color appearance indicates that only a fraction of the light can go through them. The picture below is the same as the one above, but the exposure has not been compensated to take into account polarizer losses.

A landscape with a blue sky.
Left: horizontal polarizer; middle: vertical polarizer; right: no
polarizer.
35 mm, f/5.6, 1/400 s, ISO-400.
Exposure was not adjusted and is the same for the three parts
(click to enlarge).
As one can see, the non-polarized part (on the right) is much brighter than the polarized ones (center and left). Using a polarizer requires a lot more light that usual.
When non-polarized light travels from a transparent material to another one with a higher refraction index, part of the light is refracted into the last material and part is reflected back into the first one.
Let's take the example of light coming from air (refraction index n1 = 1.00) impinging on a piece of glass (refraction index n2 = 1.52), as shown in the below picture, where non-polarized light is represented by equal arrows in all directions, polarized light by two arrows in the direction of polarization and partially polarized light by different arrows in all directions. Round arrows represent the direction of propagation of the light.

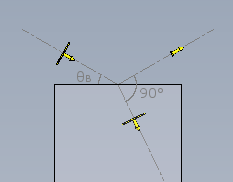
In case of reflection by a higher refractive index dielectric material, if
the incident angle is such that reflected and refracted rays are 90°
apart, the incidence angle is called Brewster's angle and the reflected light
is linearly polarized with its plane parallel to the reflection surface
(click to enlarge).
If the angle of incidence is such that the reflected and the refracted rays are 90° apart, the reflected ray is linearly polarized and its polarization is parallel to the reflective surface. When this happens, the incidence angle is called Brewster angle θB and depends on the ratio of the two refraction indexes:
θB = 90° – arctg(n2 / n1)
It's interesting to remark that at the Brewster's angle, this particular polarization is completely reflected back in the first medium. Light refracted into the second medium lacks of course this polarization (but still has all the others) and becomes partially polarized.
The good news is that if the angle of incidence is not exactly the Brewster angle, the reflected ray will only be partially polarized, but still a bit polarized, allowing using this phenomenon to be widely used in photography.
Please remark that this phenomenon only happens when the light is reflected by dielectric materials such as water or glass. When reflection occurs on a metallic surface, no Brewster angle nor refracted light exist (mirrors very often use reflective metallic surfaces).
The table below shows Brewster's angles for air-water and air-glass interfaces:
| Material | Refraction index | Brewster angle |
| Air – Water | n1 = 1.00 ; n2 = 1.33 | θB = 37° |
| Air – Glass | n1 = 1.00 ; n2 = 1.52 | θB = 33° |
Please remark that in this page angles are measured from the surface to the ray and not from the surface's normal axis to the ray which is usually used in optics.
Now, in photography, it's quite common to have reflection from windows (glass) or from water. For example, the three pictures below show the surface of a pond. The left image was taken through a horizontal polarizer, the middle one though a vertical polarizer and the left one without polarizer. As one can see, in the middle image the reflections on the surface are much weaker and one can better see what's in the water. That's because reflections on the water are mainly horizontally polarized and cannot go through a vertical polarizer. If the polarizer is horizontal, not only the reflections are not blocked at all, but part of the light coming from objects under the water (which is not polarized) is attenuated by the polarizer, emphasizing a little more the reflections, even if the result is quite similar as if no polarizer is used.

Water surface in a pond.
Left: horizontal polarizer; middle: vertical polarizer; right: no
polarizer.
35 mm, f/5.6, 1/50 s, 1/60 s, 1/200 s (respectively), ISO-400.
Exposure was adjusted to take into account polarizer losses (click to
enlarge).
We have seen that the Bewster's angle for reflections between air and water is about 37°. This is the case at about one third of the height of the image; in the top part of the image the angle is much smaller and the polarizing effect of the reflection is not noticeable. For this reason, the top part of the image is similar for all three polarizer settings.
Let's take another example. In the picture below are represented three images of the same scene: the one on the left was taken through a horizontal polarizer, the one in the middle through a vertical polarizer and the one on the right was not polarized. In front of the camera there is a glass plate angled at exactly 33° and a lighter is just behind. On the right, not visible on the image, there is a lit candle. The angle of the glass surface and the camera axis form, of course, exactly the Brewster angle, so that the reflected light of the candle is vertically polarized.

A glass in front of a lighter and a lit candle on the side.
Left: horizontal polarizer; middle: vertical polarizer; right: no
polarizer.
35 mm, f/16, 1/2 s, 1/2 s, 1/6 s (respectively), ISO-400.
Exposure was adjusted to take into account polarizer losses
(click to enlarge).
As one can see, the reflection of the candle is almost invisible on the left image since the horizontal polarizer completely blocks this reflection. If the polarizer is vertical, not only the reflections are not blocked at all, but part of the light coming from the lighter (which is not polarized) is attenuated by the polarizer, emphasizing a little more the reflections, even if the result is quite similar as if no polarizer is used.
A linear polarizer would be enough for normal photography, because what a photographer usually expects from a polarizer is a filter that blocks light which the polarization plane is perpendicular to the one of the filter and lets in only one particular plane of polarization. For this reason, polarizers for photography can be rotated about their axis to let the user choose the polarization plane he wants, exactly like linear polarizers, but they are marked "circular polarizers". Circular polarization has a "helix shape" and doesn't have a plane: rotating the polarizer around its axis would have no effect.
The problem is that some cameras have sensors (such as for the exposure meter or the autofocus) that are fooled by linearly polarized light. The solution is to use a circular polarizer instead and place it with the quarter wave plate facing the imager of the camera. The linear polarizer is on the outside and allows using the filter as a regular linear polarizer while the quarter wave plate on the inside transforms the linear polarization into a circular one that has less influence on camera sensors.
Circular polarizers work only in one direction: they have a linearly polarized side and a circular polarized side. They are composed by a linear polarizer followed by a quarter wave plate that transforms a linear polarization into a circular polarization. These layers are usually very thin coatings on a glass palate that is used as mechanical support. In the following two pictures they are represented as two separate plates for clarity but are often assembled together.

Circular polarizer as used in photography applications: the linear
polarizer is toward the scene and selects the desired linear polarization.
The quarter wave plate follows the polarizer and transform the linear
polarization into a circular one that has less influence on camera sensors
(click to enlarge).
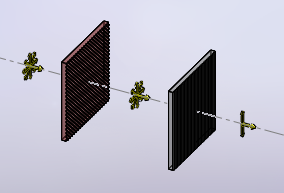
If a circular polarizer is mounted in the other way, the quarter wave
plate will have no influence on non-polarized light and the filter will
behave just like a linear polarizer.
Of course, used this way, the quarter wave plate will have an effect on
circularly polarized light and let through only the correct handedness, but
circularly polarized light is so rare in nature... (click to enlarge).
To the naked eye, a quarter wavelength plate looks perfectly transparent since it only affects the phase of the light. Cellophane has often a quarter wave plate behavior, but this depends on its thickness. Still it has very interesting properties on circularly polarized light.
If you are wondering how you can determine if your polarizer is linear or circular (if it's not written on it), is very easy: all you need is a (metallic) mirror. The vast majority of bathroom mirrors are metallic mirrors with a glass in front of them and work just fine. Just beware of plastic (toy) mirrors that may have strange effects on polarization. A shiny metal surface also does perfectly the job.
Reflections on metals do not change linear polarizations, but invert the phase transforming a left handed circular polarization in a right handed one and vice versa.
So, look at the mirror through your polarizer: if you can see your eye through the polarizer you have a linear polarizer or a circular polarizer with the quarter wave plate toward your eye. Now flip the filter over, if it appears black, it's a circular polarizer and the quarter wave plate is toward the mirror.
With a linear polarizer toward the mirror, light coming from the polarizer and travelling toward the mirror is linearly polarized; when reflected it's still linearly polarized in the same way as before and can go through the polarizer again, so that you can see your eye.
If you have a circular polarizer with the quarter wave plate towards the mirror, light coming from the polarizer travelling toward the mirror is circularly polarized. The mirror reverses the handedness of the circular polarization and the reflected light cannot go through the polarizer again, so you cannot see your eye and the polarizer appears black.

Looking at a mirror through a polarizer.
Left: linear polarizer or circular polarizer with quarter wave plate towards
the observer.
Right: circular polarizer with quarter wave plate toward the mirror.
70 mm, f/22, 1 s, ISO-400 (click to enlarge).
In the above picture there is a circular polarizer at some distance in front of the lens and a mirror a bit further away. In the left half the circular polarizer is oriented with the quarter wave plate facing the camera. This is the normal way you mount circular polarizer on cameras. Please remark that you can see the camera reflected in the mirror. A pure linear polarizer would behave in this same way.
On the right half of the image the polarizer was flipped around and the quarter wave plate is now facing the mirror. One can remark how the reflected image of the polarizer is now black and it's not possible anymore to see through.
Some basic principles of polarization and their application in photography have been explained. Wave polarization is a very broad topic and the goal of this page is not to cover it in an exhaustive way. A lot of more interesting information can be found in the books listed in the bibliography section below.
| [1] | Eugene Hecht. Optics. 4th Edition, Addison Wesley, 2002, section 4.2.1. |
| [2] | Eugene Hecht. Optics. 4th Edition, Addison Wesley, 2002, chapter 8. |
| Home | Optics | Page hits: 085989 | Created: 01.2006 | Last update: 03.2014 |